エクセルで cos の値が 05 になる θ を 度 で求める式は =degrees(acos(05)) で結果は ;ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる: sin θ = ± 1 − cos 2 θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^{2}\theta }}}三角関数の合成公式の証明と応用 レベル ★ 基礎 三角比・三角関数 更新日時 三角関数の合成公式とは,sin と cos が混ざった式を,sin だけで表すための,以下のような公式です。 a sin θ b cos θ = a 2 b 2 sin ( θ α) a\sin\thetab\cos\theta

漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100
Cos(θ+π/2)=-sinθ なぜ
Cos(θ+π/2)=-sinθ なぜ- 問題 0≦θ≦π/2 かつsinθcosθ=1/4 とする。さらに、sinθ>cosθとするとき、次の式の値を求めなさい。ただし、途中式を書くこと。 この問題の解き方の手順がちんぷんかんぷんです。作問者が言うには、「ずいぶん意地悪な問題ですよ。 さあ「sinθ」と「θ」の基本的かつ重要な性質が分かったところで、この2つを結びつけていこう。 ところでこの近似「sinθ ≒ θ」には、 重要な前提条件 がある。 それは、 θがものすごく小さい ということだ。 θ が 1°とか 2° とか、そういうときは使えるって感じで、θが小さければ小さい



三角関数 どうしてsin P 2 8 がcos8になるんです Yahoo 知恵袋
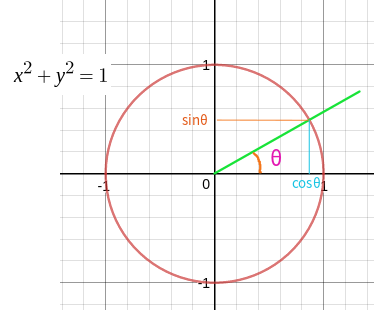
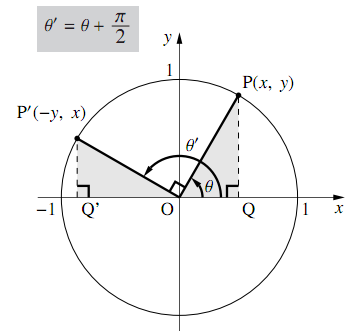
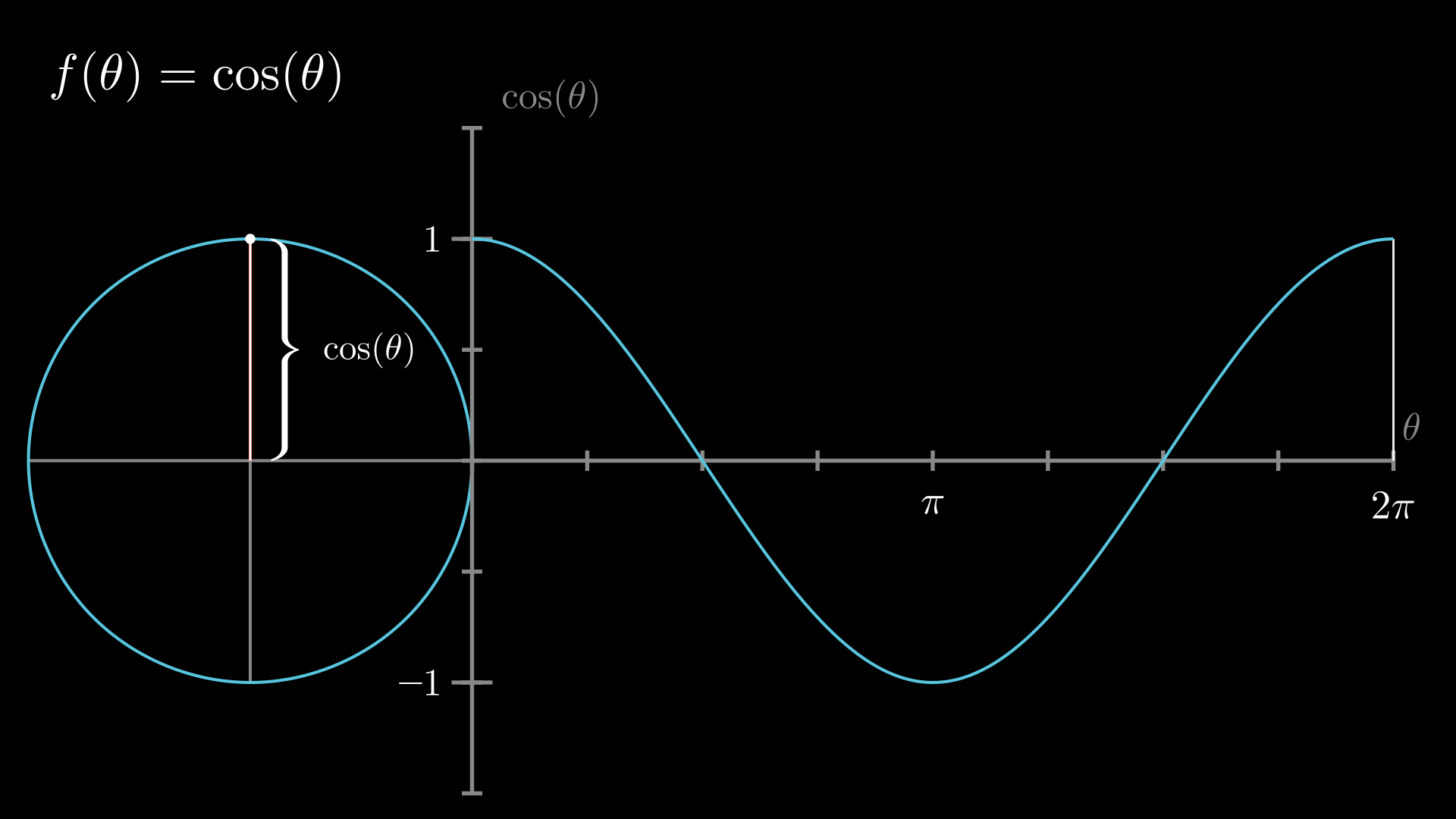
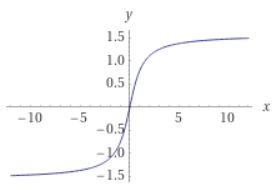
ここでθ=xπ/2 とすると ①= (1/2)θcosθ/sinθ θ≒0で θ≒sinθ、つまり lim θ→0θ/sinθ=1 を利用すると lim θ→0①= (1/2)lim θ→0θ/sinθ=1/2 というわけで、極限=0は間そして結論から言うと、タイトルの通り sin の微分は cos になります。 それでは、なぜそうなるのでしょうか? (θ)の長さは、θの値が 0 から π(180度)の間は正の値になり、π(180度)から 2π(360度)の間は負の値になります。 2 sinの微分はcosθ, and the points (x,y)=(cosθ, sinθ), that are most commonly used (also see table in the following section) Fig3 Most commonly used angles and points of the unit circle Note For θ in quadrant I, sinθ>0, cosθ >0;
数学・算数 三角関数 問題 次の式を簡単にせよ。 cos(π/2 θ)cos(θ)cos(π/2 θ)cos(πθ) 解答 (与式)=sinθcosθsinθcosθ 質問Noえっと、 a cos(θ)^2 b sin(θ)^2というのは a(cosθ)^2b(sinθ)^2ですよね? 答えがcosで表されているので、(sinθ)^2をcosで表現すると 1(cosθ)^2です すると a(cosθ)^2b(sinθ)^2 =a(cosθ)^2b{1(cosθ)^2} 整理して =(ab)(cosθ)^2b ここで、二倍角を使います cos2θ=2(cosθ)^21 ですので、 (cosθ)^2=(cos2θ1)/2 です sin,cos,tan,の問題 sinθ/1+cosθ + 1/tanθという問題と (1tanθ^2)cosθ^22sinθ^2というもんだいなんですけど、表現があってるのかわからないんですけど^2は、2乗の意味で使いました。お願いします。
三角関数の性質の、 sin(θπ)=sinθや、 cos(θπ/2)=sinθ、 tan(θ)=tanθなどは、どうしてそうなるんですか? 全部暗記しなくてはならないんでしょうか?と から は定義されませんと言ってしまえばいいのですが、こんなことは承知の上での質問ですね。 何故、このような疑問を持ったのでしょうか。有名な という等式のように、何か見方を変えると定義できるのではないかということでしょうか。2 is the velocity of the target particle in the center of mass system, then v 2 = V v0 2, represented in Fig3 Figure 3 Graphical vector sum v 2 = v0 2 V The components of the vector sum are equations relating the magnitudes of the vectors and the angles φ,Θ, similar to the equaitons (3106) for m 1 v 2 sinφ = v0 2 sinΘ v 2 cosφ = V



三角関数 初等数学 基礎からの数学入門




数学 Sina Cos P 2 A なぜこのような式になるのでし Okwave
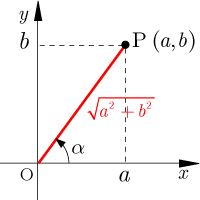
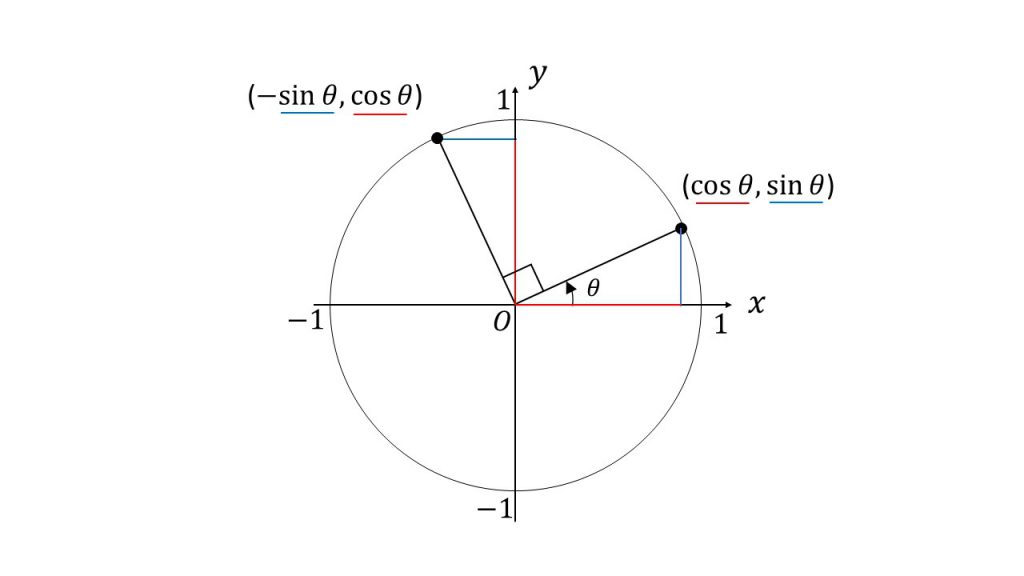
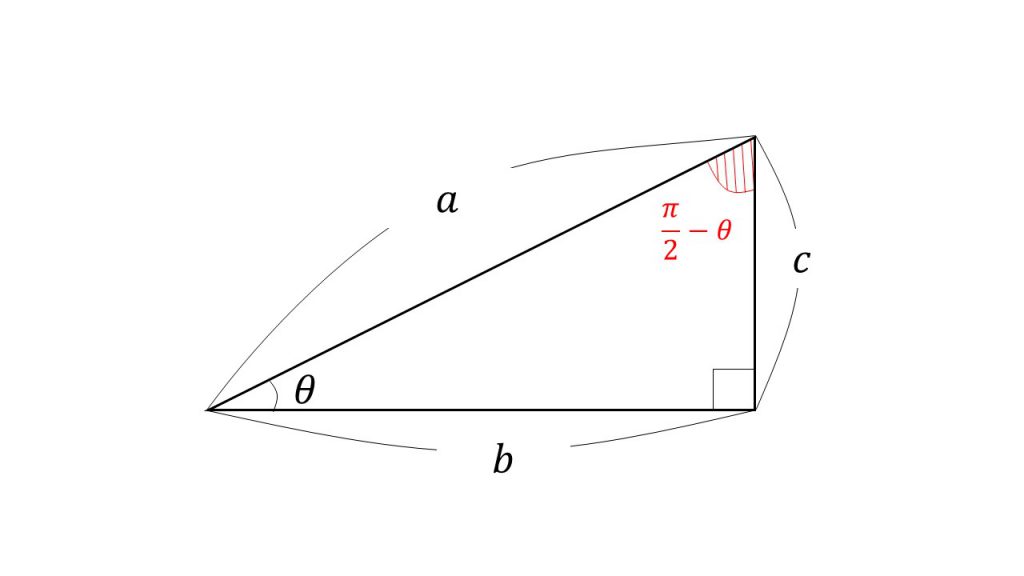
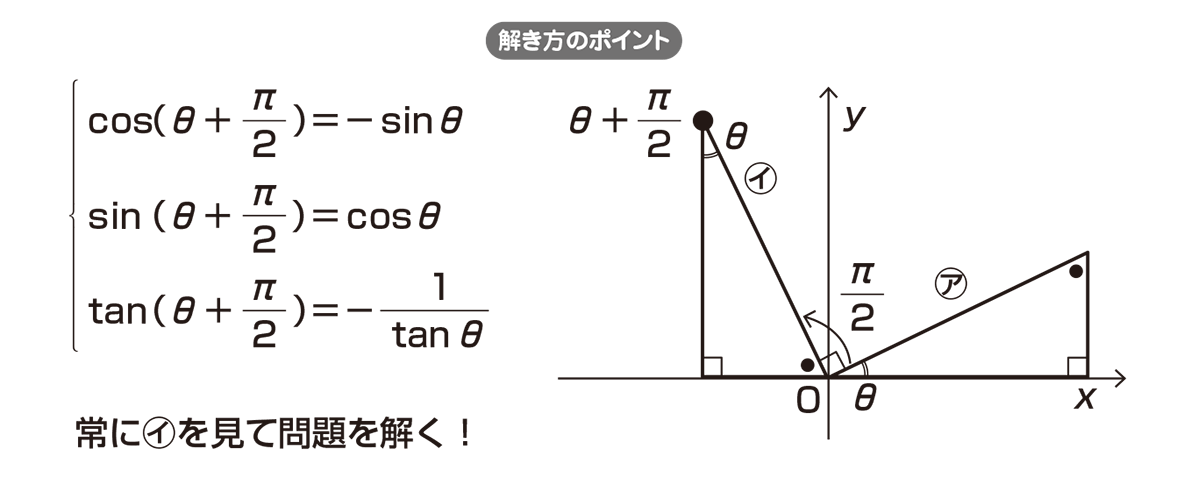
と書けることになります. しかし,一般には asin θbcos θ のように与えられた係数, a, b がそのままで一つの角度 α の三角関数 cos α, sin α に等しいことはめったにありません. 右図のように a, b が2辺となっている直角三角形を考えると,1) −2sin(θ π/2)sin(θπ/2) , 2) 2cos(θ π/2)sin(θπ/2) , 3) 2cos(θ π/2)cos(θπ/2) , 4) None of the Above 正しいイメージを持つことができない生徒は、なぜそのような誤解をしているのか、上手く説明できないことも多いです。 (π/2-θ)=cosθ cos(π/2-θ)=sinθ tan(π/2-θ)=1/tanθ



三角関数の性質を単位円で理解する 8 2np 8 P 8 P 2 8 大学受験の王道



初心者向け 三角関数と指数 対数関数の 巡回性 について Qiita
0103 sinθ=√1cosθ^2という公式について質問です。 この公式は、どの三角関数の公式から計算されたものなのでしょうか? sin^2x= (1cos (2x))/2から計算されていると思ったのですが(あっているかはわかりません)どう変形していいのかわからず困っ符号にも注意を! では、直角三角形イで (θπ/2)の三角比を考えましょう。 「底辺」と「高さ」が入れ替わっているので、 cos (θπ/2)=sinθ sin (θπ/2)=cosθ tan (θπ/2)=1/tanθ と表せます。 符号の変化にも注意してください。 では、ポイントを使って実際に問題を解いてみましょう。電卓などでアークコサインを cos1 と表記する場合があります↓ 関連ページ: 『cos1アークコサインを使用した




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ



三角関数の性質を単位円で理解する 8 2np 8 P 8 P 2 8 大学受験の王道
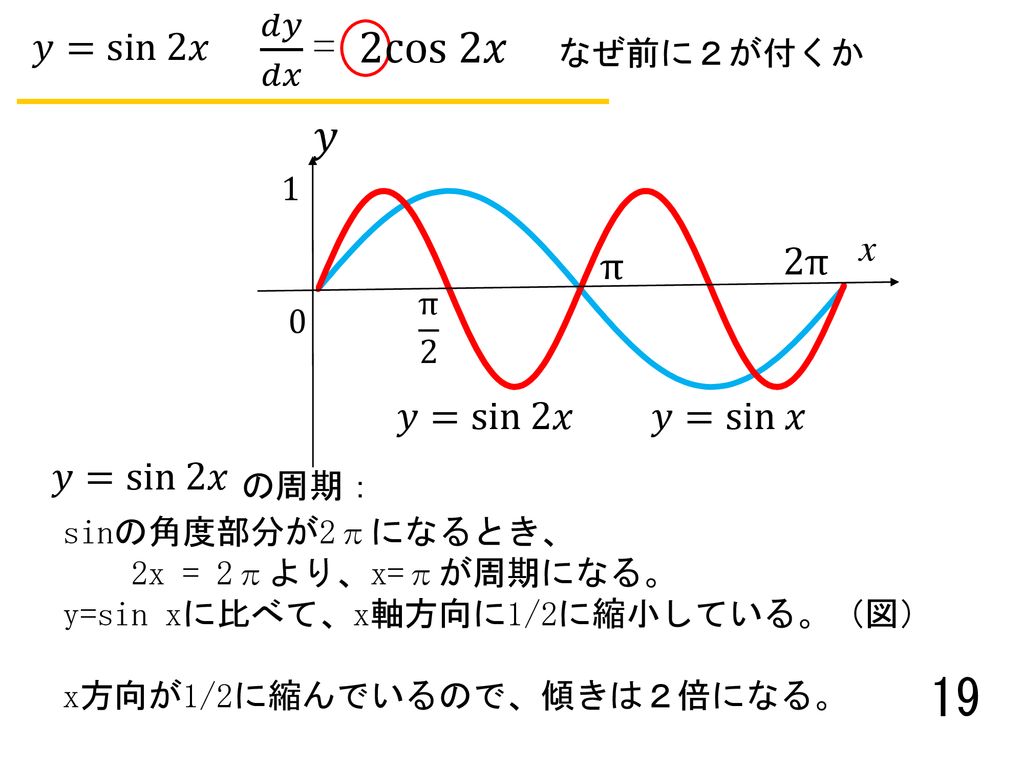
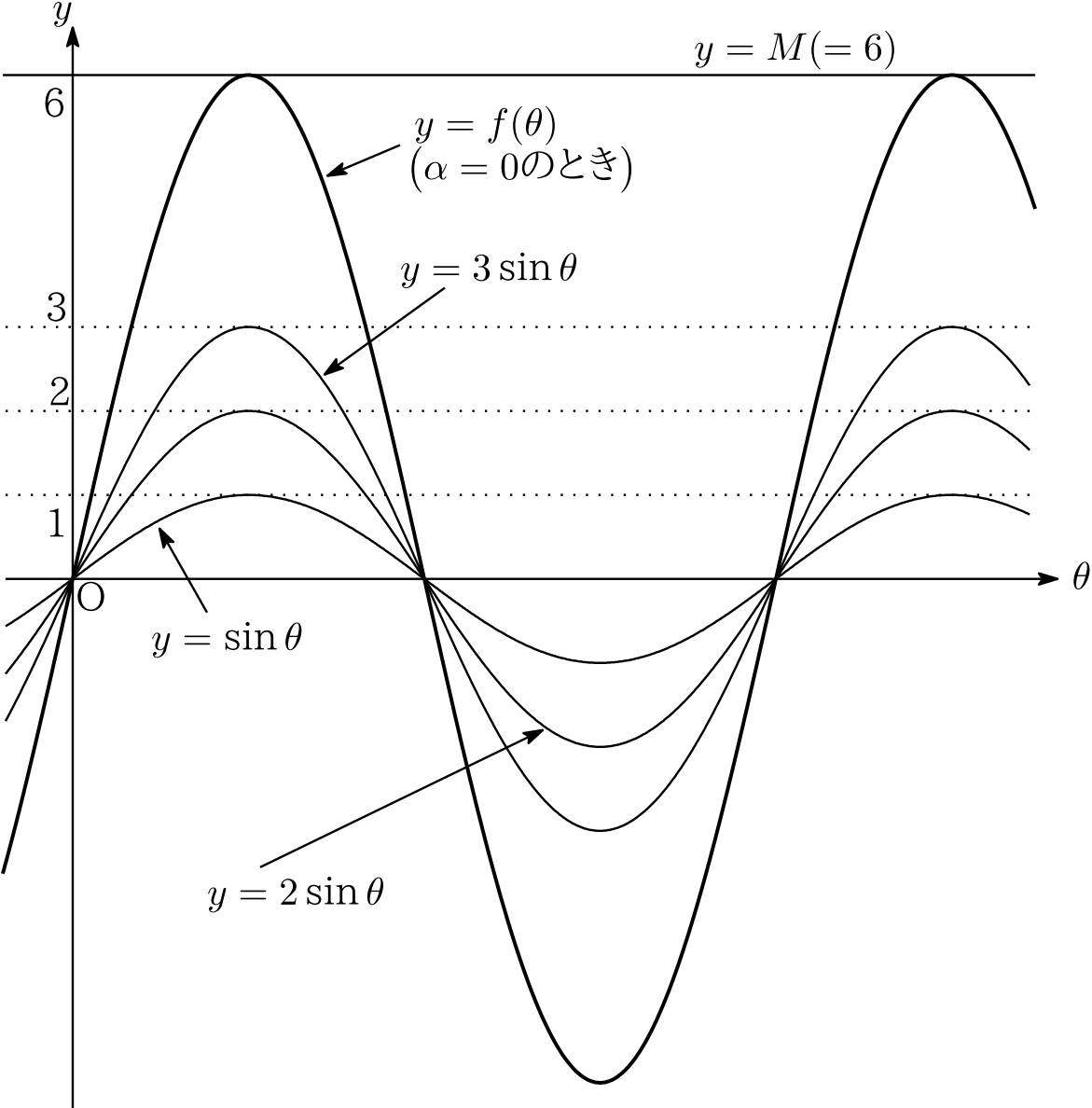
θ の定義式から求められます。 2つ目は sin 2 θ cos 2 θ = 1 。 これは、 三平方の定理 から求められます。 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 直角三角形において、「直角」をはさむ2つの辺の長さを a, b 、斜辺の長さを c としたとき \ (a^2b^2 3つ目は tan 2Y= sin 2(θ −30 °) と変形する。 このように変形すると、 y= sin (2 θ −60 °) のグラフは y= sin 2 θ のグラフを θ の正の向きに 30 ° だけ平行移動したものであることが分かる。 例7 y= cos (3 θ 180 °) は y= cos 3(θ 60 °) と変形できるから数学・算数 数学II三角関数 下の問題の導き方がわかりません。 sinθcosθ から sinθcosθ の求め方はわかるのですが、sinθcosθ から sinθcosθ を解くことがど 質問No



三角形の辺の比による三角関数の定義




If Sin 8 3 5 And P 8 3p 2 Then What Is Tan 8 Quora
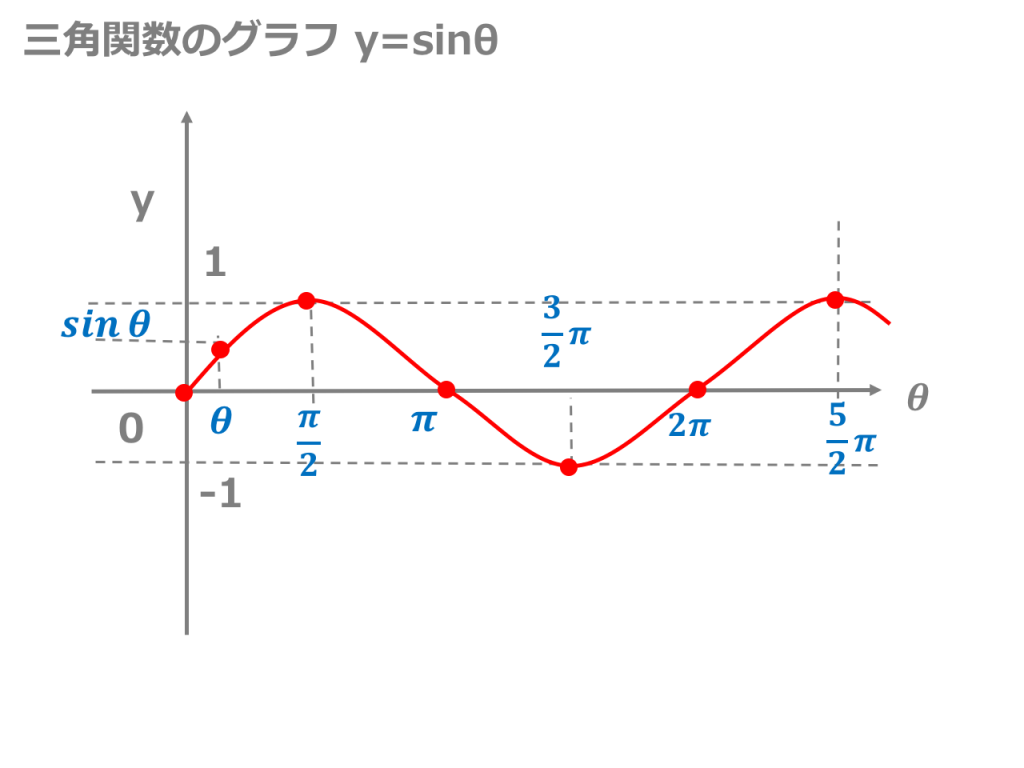
楕円C x=acosθ y=bsinθ (0≦θ またy=tanθのグラフで注意する点は 周期が2πではなく、πである点です。 sinθやcosθのグラフと一緒にしないように注意しましょう。 三角関数のグラフの特徴 \(\sin(θ)=sinθ,cos(θ)=cosθ,tan(θ)=tanθ\)よりそれぞれのグラフについていかのことが成り立ちます。C^2 = a^2 b^2 2ab cos 球面三角法 球面の三角形ABCの内角をa,b,c, 対辺をA,B,Cとするとき、次のような関係が
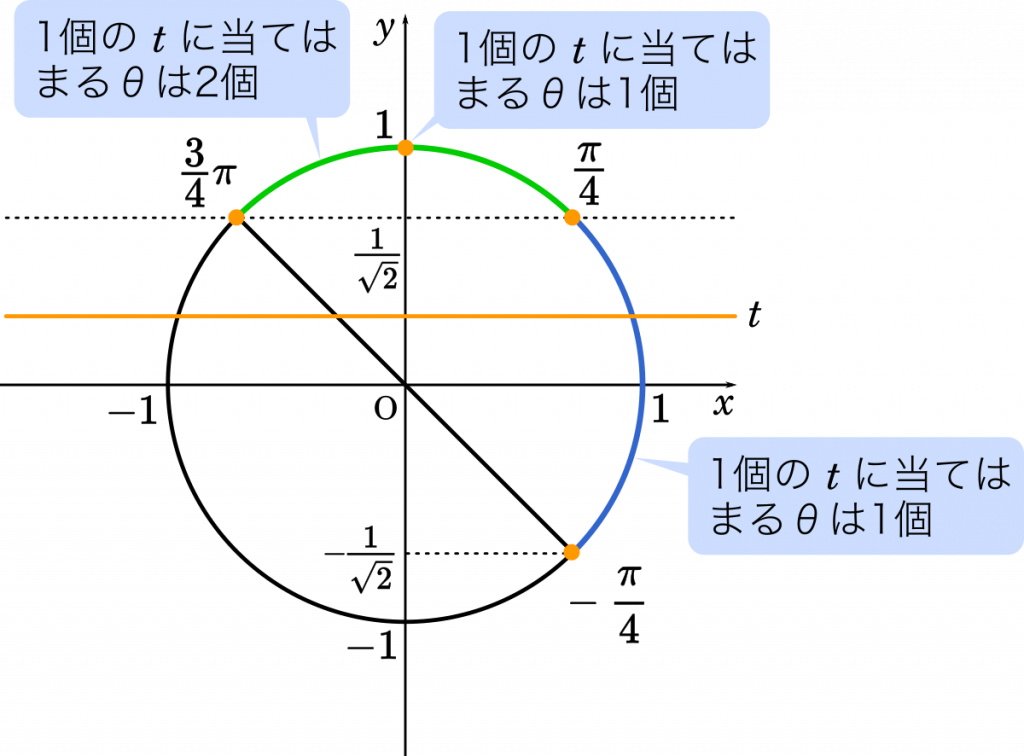



北海道大文系第2問 数iib三角関数 一つのsinに値に当てはまる8が1個のときと2個のときを判別する Mm参考書



3
三角関数の角度を求める公式と計算 三角関数の角度を求める公式を下記に示します。 それぞれ「アークサイン」「アークコサイン」「アークタンジェント」といいます。 下式のyの値が同じでもSin、cos、tanごとに角度θの値は変わります。 三角関数の2 ´ isin ³ θ π 2 ´´ (∵定理12) となり、iz は点P(z)から位相が π 2 rad進んだ点の座標であることがわかります。同様に、−iz を計算すると、 −iz = −ir(cosθisinθ)=r(−icosθ(−i2)sinθ) = r(i(−cosθ)sinθ)=r(sinθi(−cosθ)) = r ³ cos ³ θ− π 2 ´ isin ³ θ− π 2 ´´ (∵π 12 exactly 2 Prove the identity cos θ π 2 = −sinθ 3 Prove the identity sin4xsin2x = 2sin3xcosx 4 Find the value of sin − 5π 12 exactly by using the sine of a sum identity This problem shows you a method to determine exactly the trig functions at angles other than the special angles on the unit circle Page 1 of 4




三角関数についてです 写真の 2 についてなのですが なぜt P 4なの 数学 教えて Goo



数 三角関数の合成と方程式の問題です 2 がわかりません 解答解 Yahoo 知恵袋
(1)cos(90θ)cosθcos(90θ)cos(180θ) =sinθcosθsinθcosθ =0 (2)sin75sin1cos150cos165 =cos(9075)sin(1801){cos()}{cos()} =cos15*sin60cos30cos15 =√3 (1)はcos(90θ)=sinθをとりあえず置き換えて、これ±0になりそうだな、と思って感でやったらできましたが、(2)はFor θ in quadrant II, sinθ>0, cosθAcos は指定の cos の値になる θ を求めます;
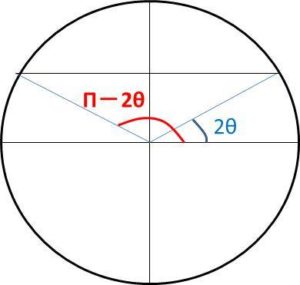



Sin28 Cos8 Sin2x Cosx やsin28 Sin8 Sin2x Sinx の解き方は Sin28 Sin38 Sin2x Sin3x の計算問題を解いてみよう ウルトラフリーダム




Cos P 2 8 はなぜ Sin8なのですか Clear




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
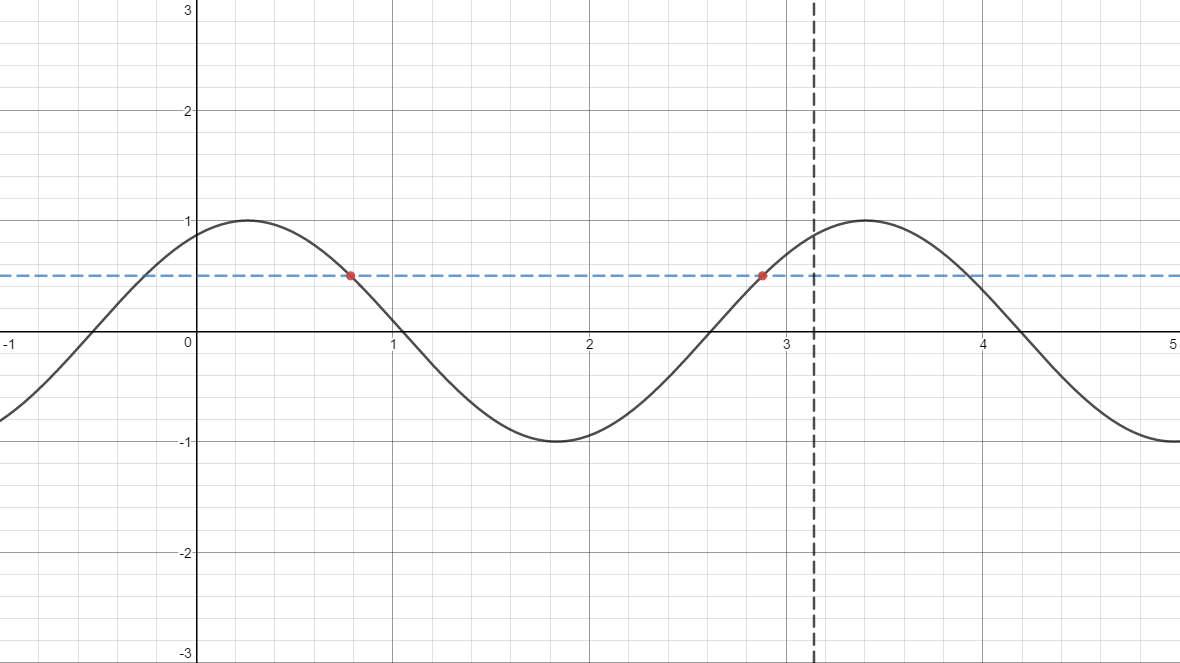



Question Ac026 Socratic
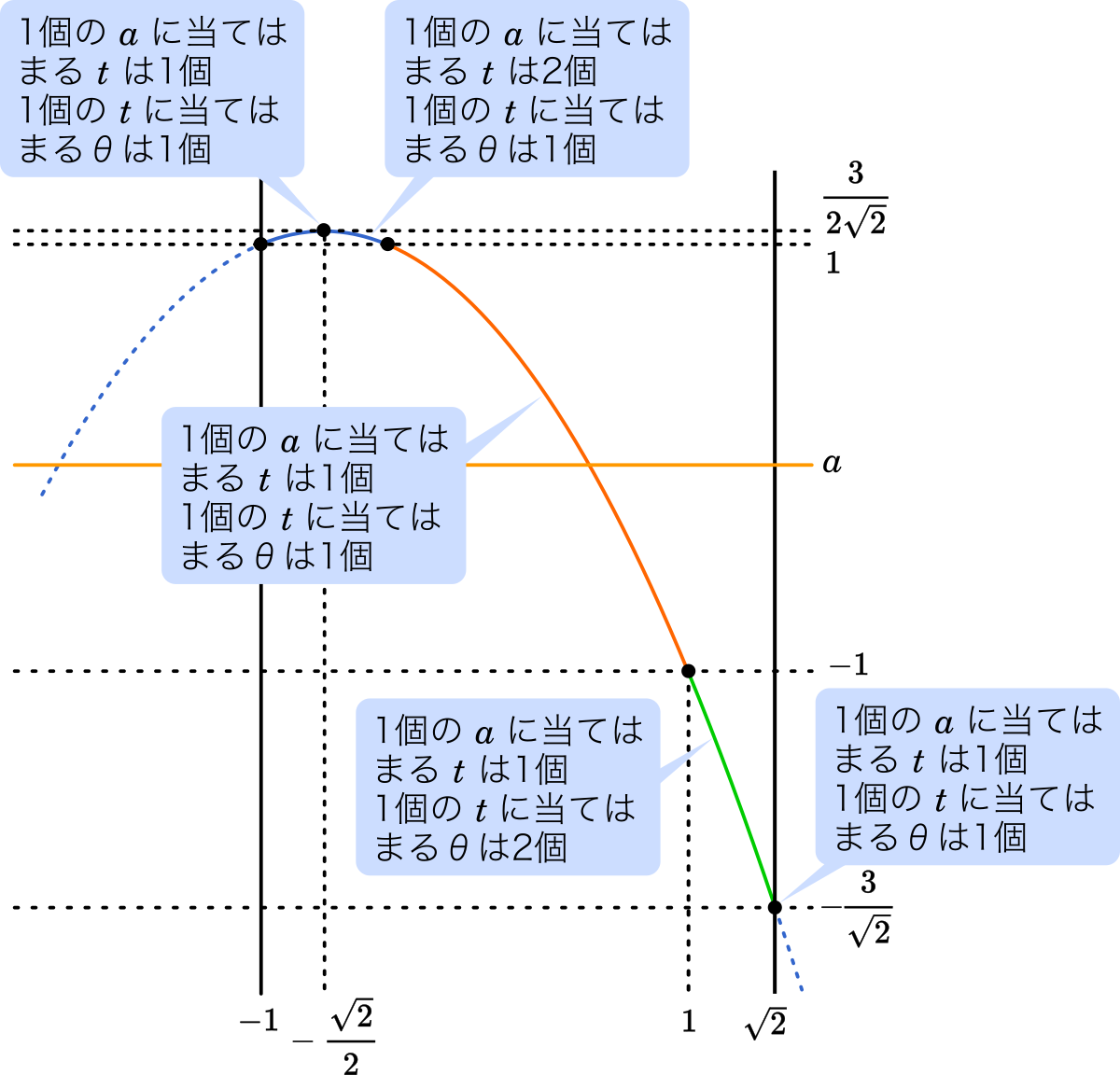



北海道大文系第2問 数iib三角関数 一つのsinに値に当てはまる8が1個のときと2個のときを判別する Mm参考書




漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100



Sin P 2 8 の考え方がわかりません 僕なりの考え方はsin P Yahoo 知恵袋




2倍角の公式と半角の公式 おいしい数学



三角関数の性質を単位円で理解する 8 2np 8 P 8 P 2 8 大学受験の王道




先程答えてくださった人には申し訳ないですが理解できなかったので質問させていただきます Clear



Http Lambda Phys Tohoku Ac Jp Miwa9 Monte Carlo Montecarlo2 Pdf




なぜsin 8 P 2 Cos8になるのでしょうか Clear



8 P 2の三角関数 数学ii フリー教材開発コミュニティ Ftext




数学 Sina Cos P 2 A なぜこのような式になるのでし Okwave



3分でわかる 三角関数のグラフの描き方 合格サプリ



振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download




16 合成公式はsinだけじゃないんです 医学生gの数学ノート




Y Sin 28 P 2 のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア



Sin 8 2分のp がcos8になる理由がわからないのだか Yahoo 知恵袋
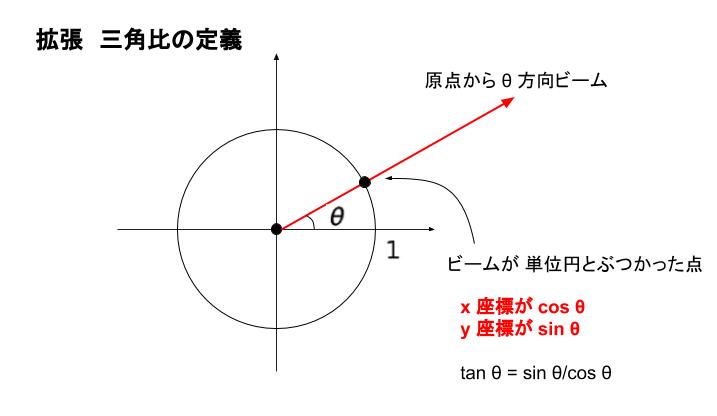



三角関数 薬学 これでok
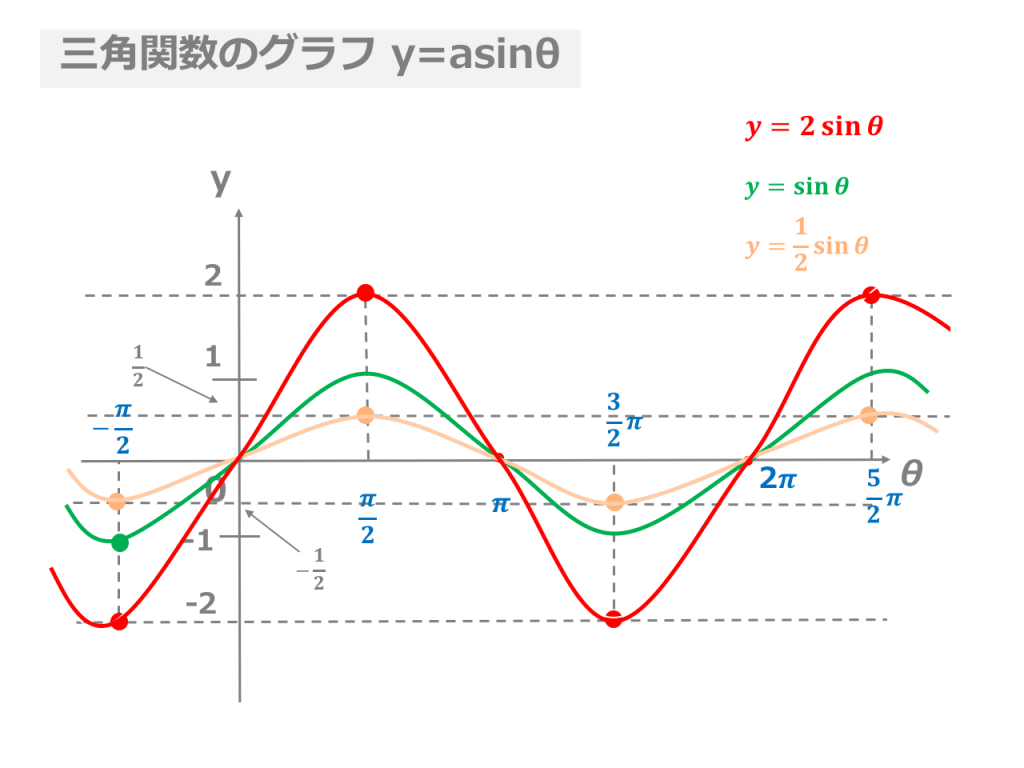



3分でわかる 三角関数のグラフの描き方 合格サプリ




極方程式の面積 扇形積分 おいしい数学




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
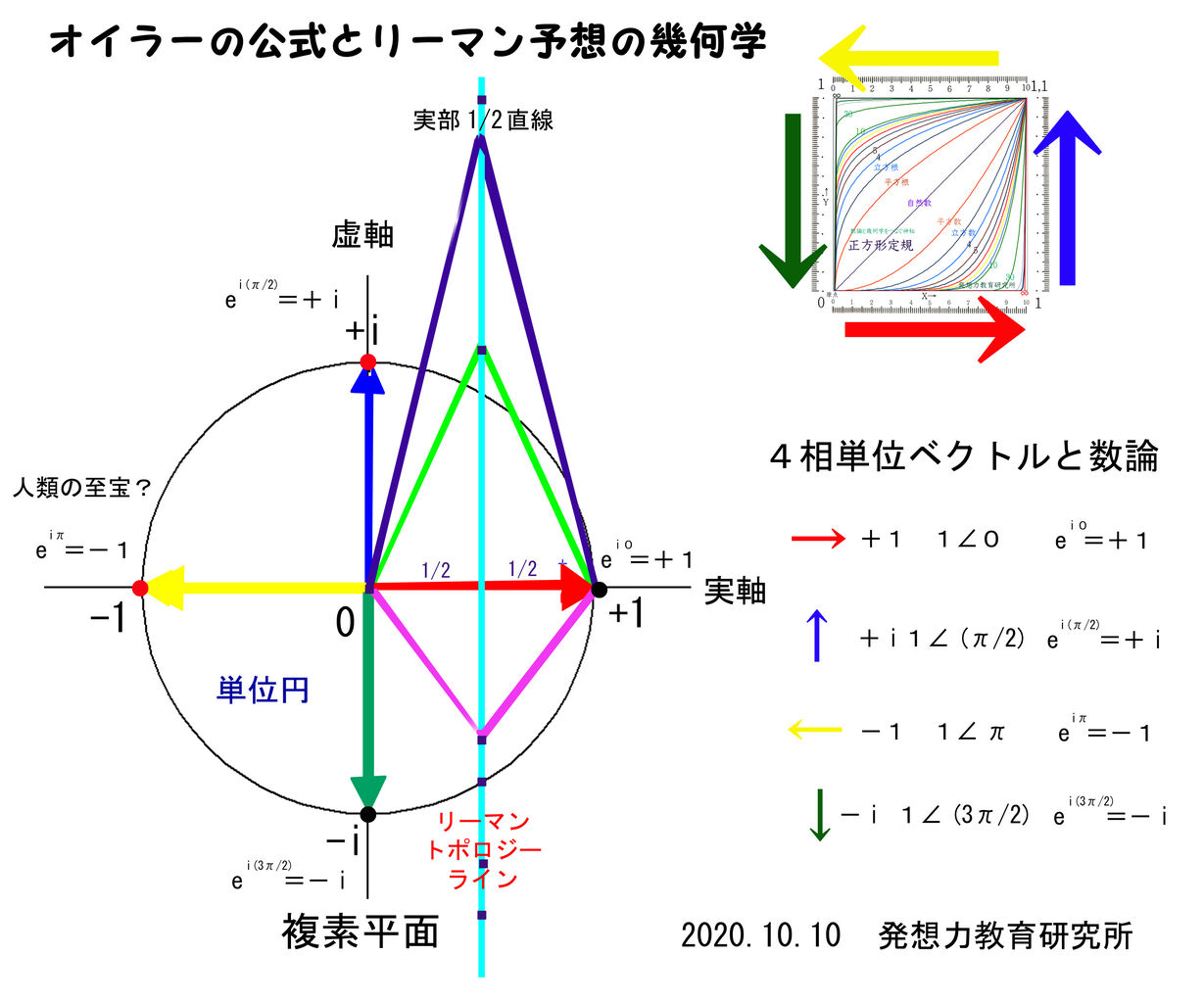



オイラーの公式 E I8 Cos8 I Sin 8 で絶対値 Cos8 2 Sin8 2 1と言えるのは8 0 90 180 270 の時だけである 発想力教育研究所 素数誕生のメカニズム



3
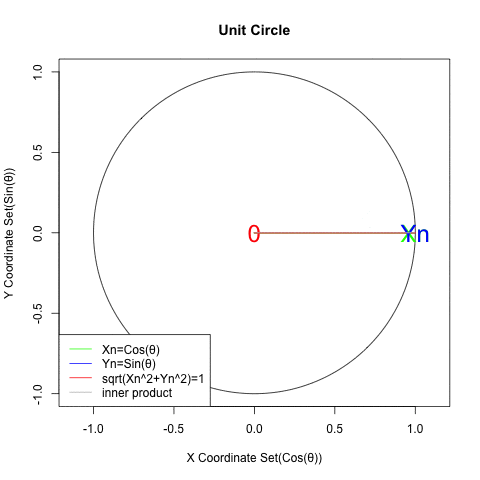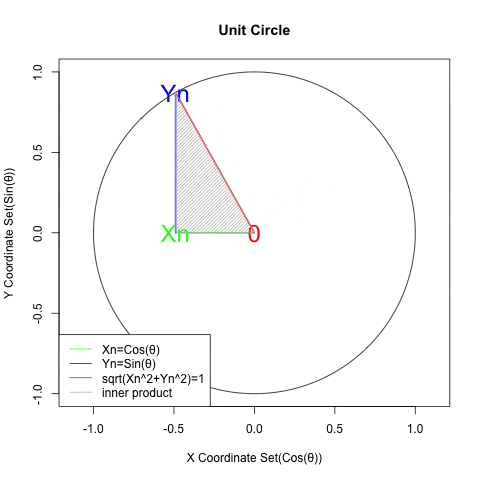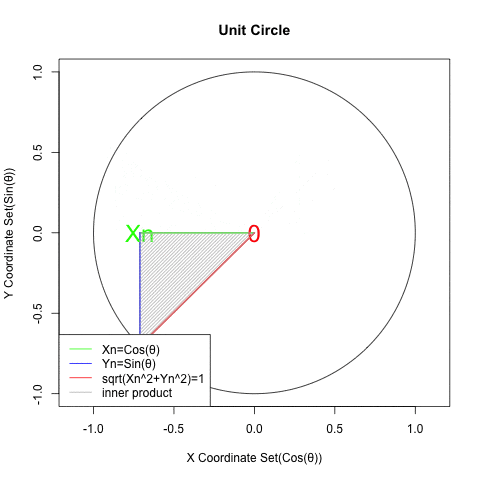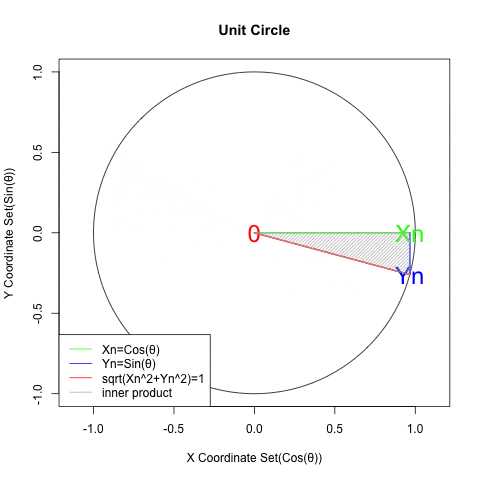



初心者向け 三角関数と指数 対数関数の 巡回性 について Qiita
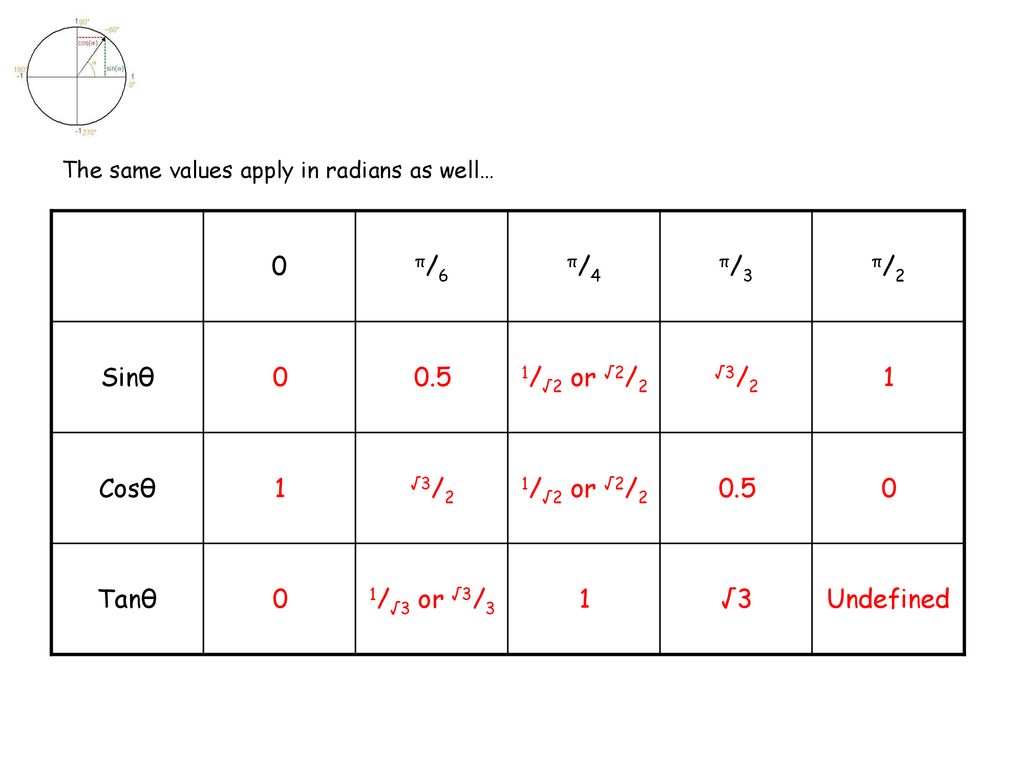



Trigonometry Inverse Functions Ppt Download



三角関数 どうしてsin P 2 8 がcos8になるんです Yahoo 知恵袋



三角関数の合成とは 公式 証明 最大最小や範囲の問題 受験辞典




三角関数を思い出してみる どこでもサイエンス 147 Tech




共通テスト 数学ii 数学b 18年度プレテスト 第1問 1 解説 ページ 2 なかけんの数学ノート
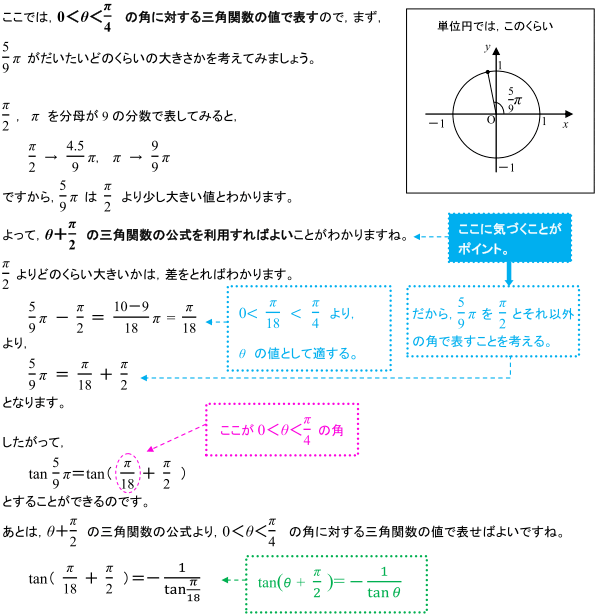



0 8 P 4 の角に対する三角関数での表し方 数学 苦手解決q A 進研ゼミ高校講座




1 Cos8 1の時8 0になるのはなぜですか 2 Cos8 0で2ぶんのp 高校 教えて Goo



If Pi 2 8 P And Sin 8 4 5 Find The Exact Value Of Cos8 And Cot8 Socratic




8 P 2 8 P三角関数の公式と導き方




どうして三角関数で度数法じゃなくて弧度法を使うの シャンのいろいろ2




三角関数 って 何でしたっけ Sin サイン Cos コサイン Tan タンジェント ニッセイ基礎研究所
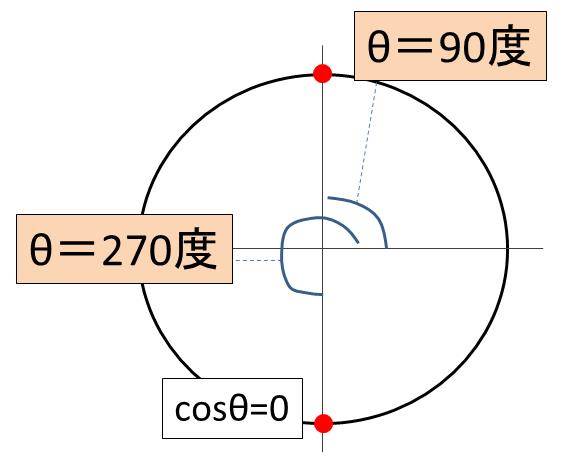



Cos8 0 やcos8 1の角度 8の値 は何度か Sin8 0 やsin8 1の角度 8の値 は 単位円 ウルトラフリーダム
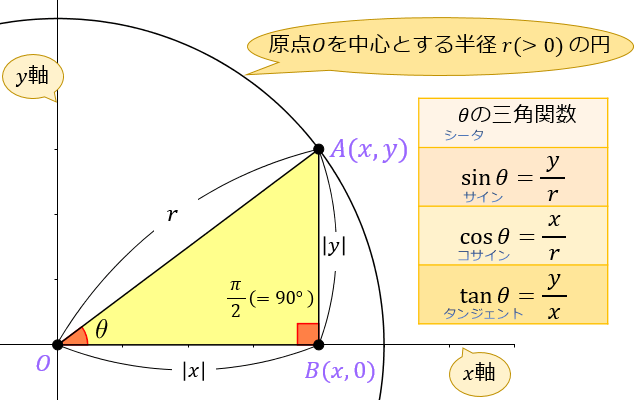



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ




弧度法が分からない人へ P 180 になる理由をイラストで解説




三角関数の合成公式 三角関数の公式一覧




高校 数学 三角関数11 8 P 2 17分 Youtube
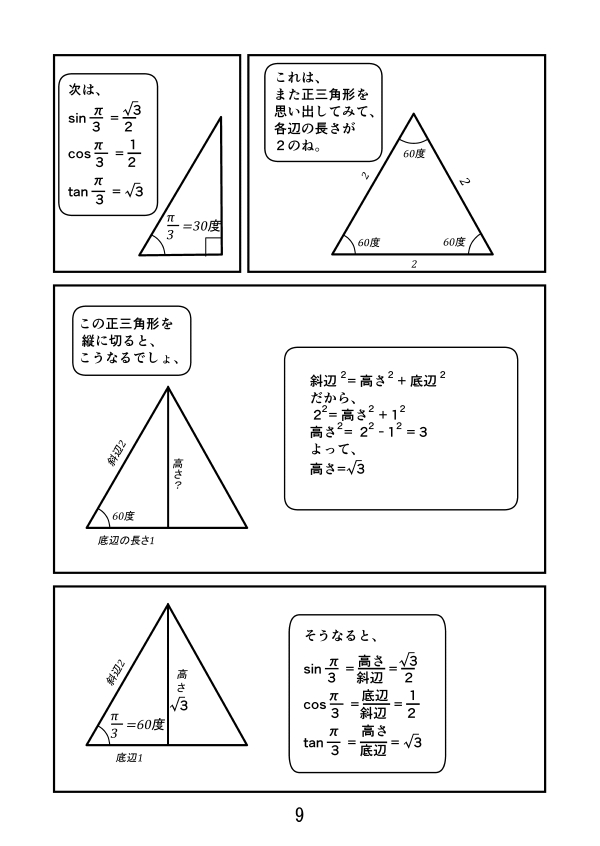



漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100



三角関数 どうしてsin P 2 8 がcos8になるんです Yahoo 知恵袋



3




三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ



48s96ub7b0z5f Net Sankakukansuu Seishitsu




角度の場合分けについて 数学 苦手解決q A 進研ゼミ高校講座
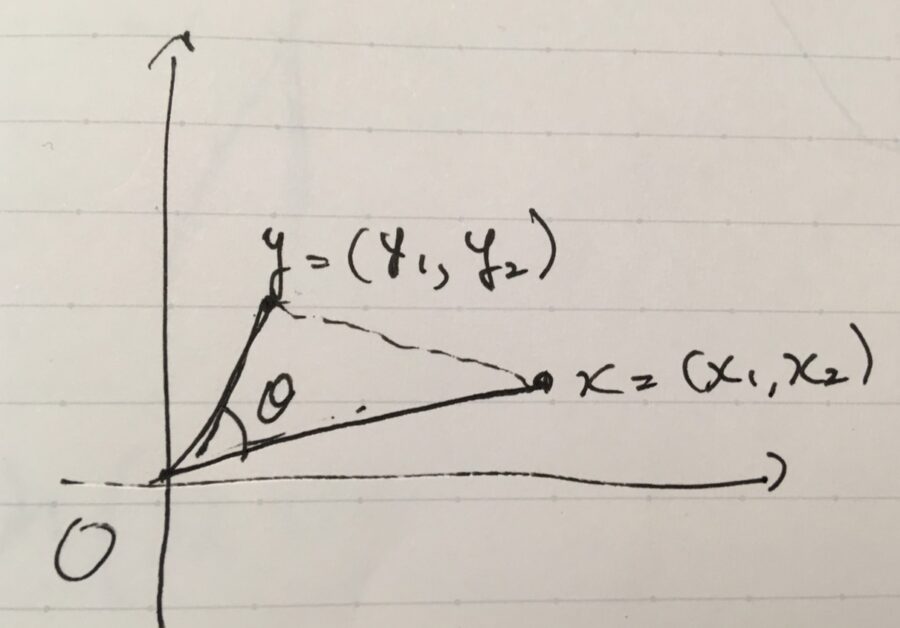



余弦定理とベクトルの内積の関係 なぜコサインか 趣味の大学数学
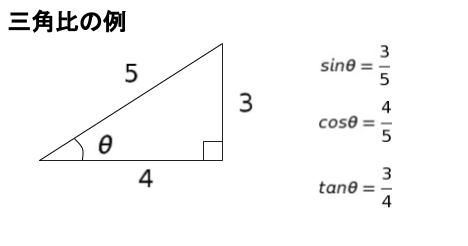



三角関数 薬学 これでok




半角公式が一目でわかる 証明 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ
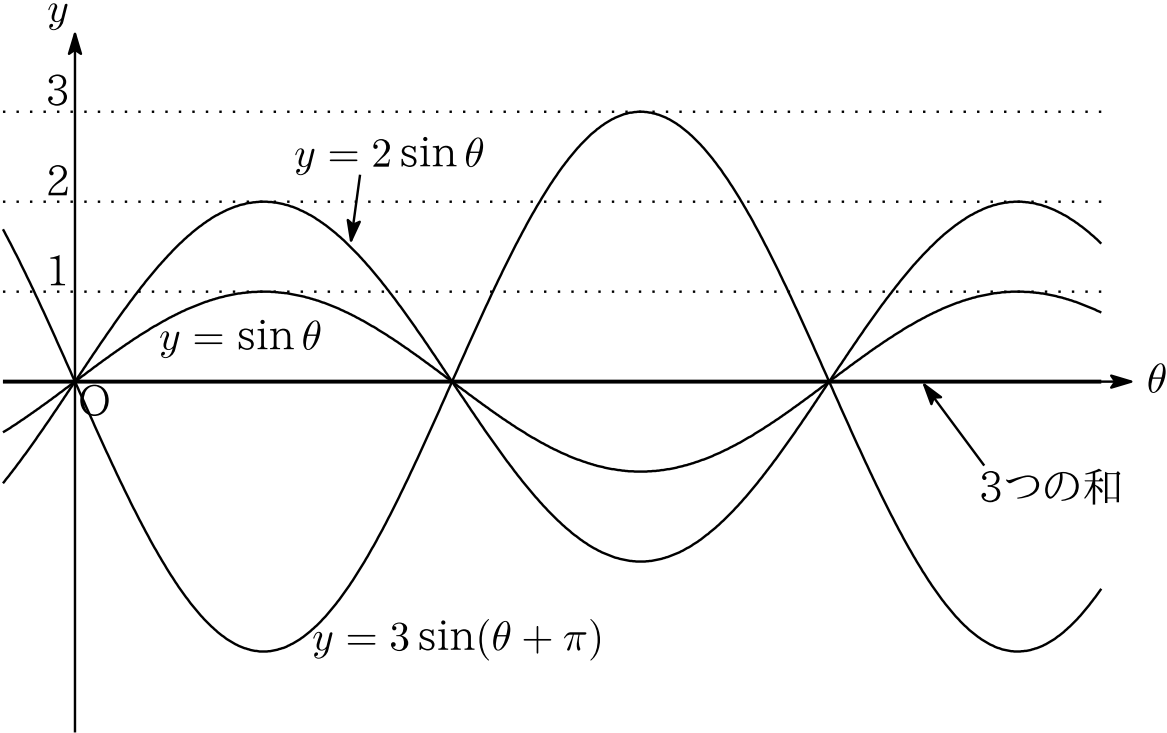



合格る一題 うかる一題 第1問 解答 解説 河合塾マナビス
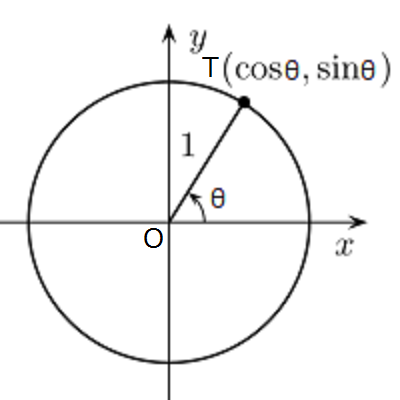



正弦 Sin 余弦 Cos 正接 Tan の求め方 しかくのいろは
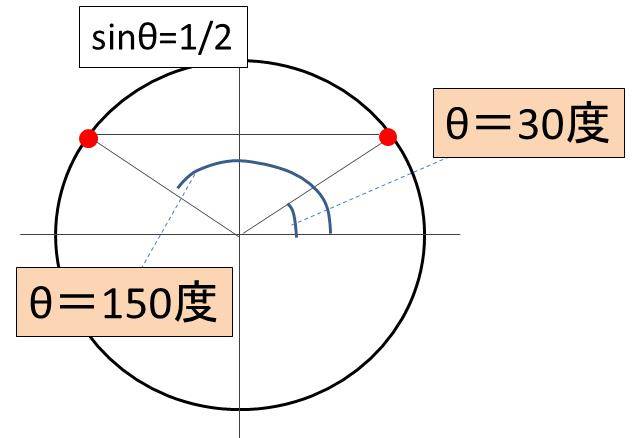



Sin8 1 2の角度 8の値 は Sin8 ルート3 2やsin8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム
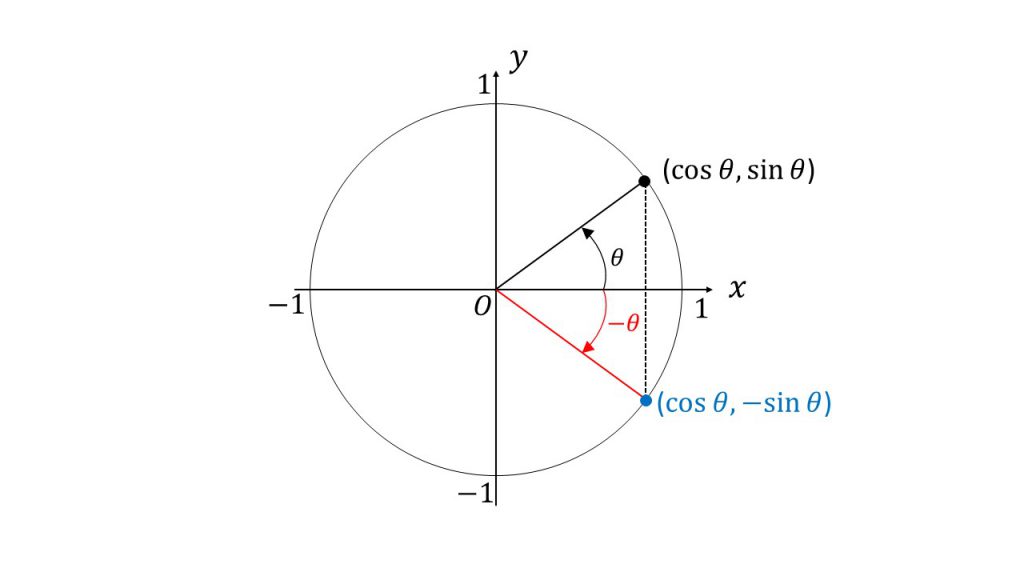



三角関数の性質を単位円で理解する 8 2np 8 P 8 P 2 8 大学受験の王道
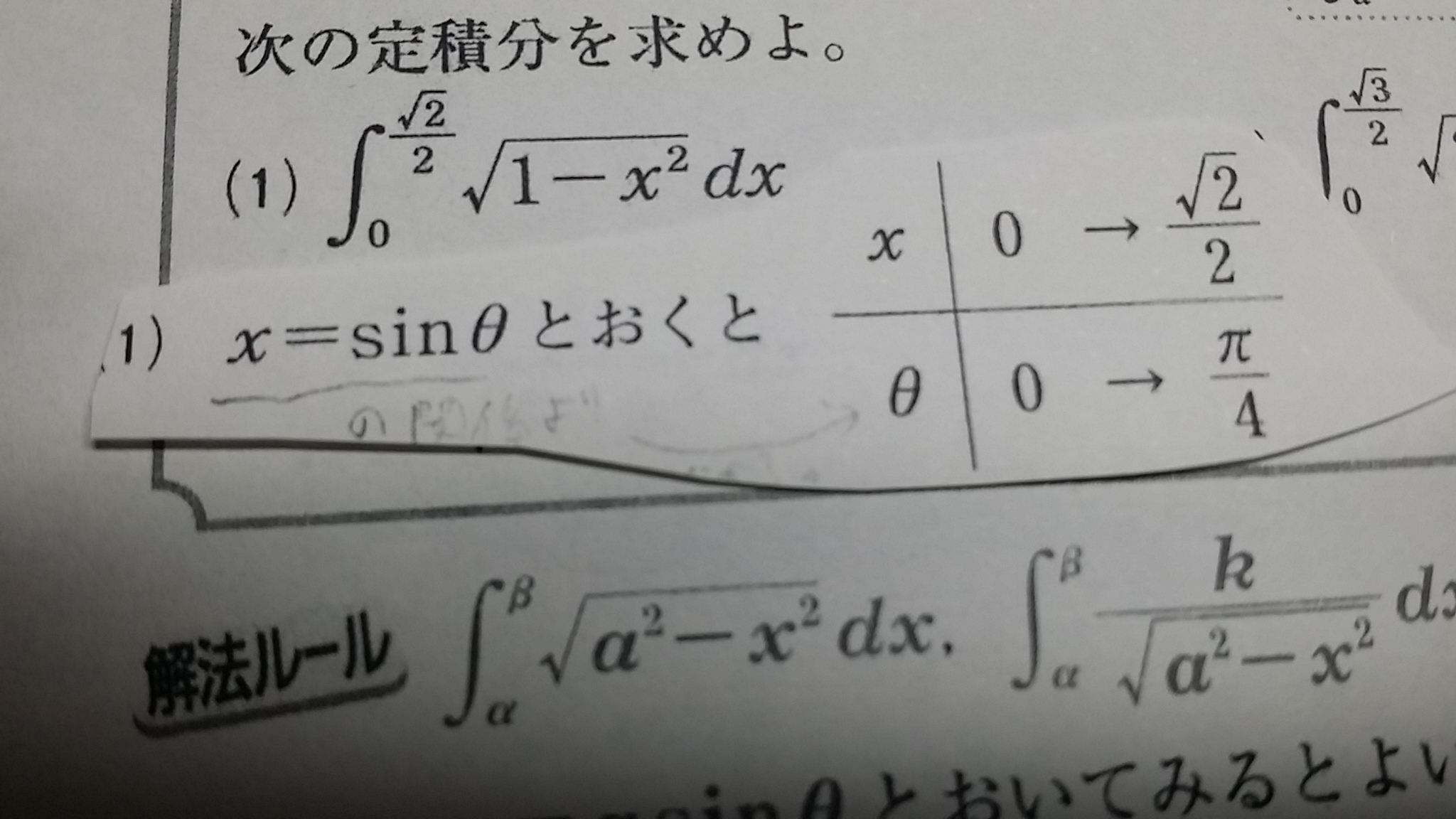



Sin8の8の範囲はなんで0 8 P 2と Okwave
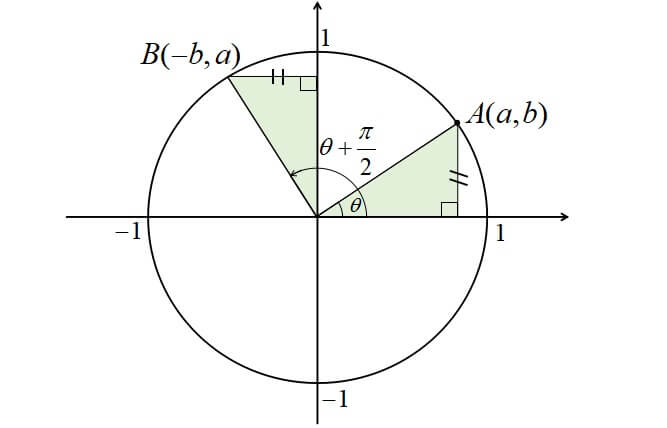



8 P 2 8 P三角関数の公式と導き方



Cosの微分が Sinになる理由を誰でも簡単に理解できるように解説 Headboost



三角関数 って 何でしたっけ Sin サイン Cos コサイン Tan タンジェント ニッセイ基礎研究所



三角関数についてですが Tan 8 P 2 1 Tan8となる理由を教えて Yahoo 知恵袋




三角関数の公式一覧



高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット



合格る一題 うかる一題 第1問 解答 解説 河合塾マナビス
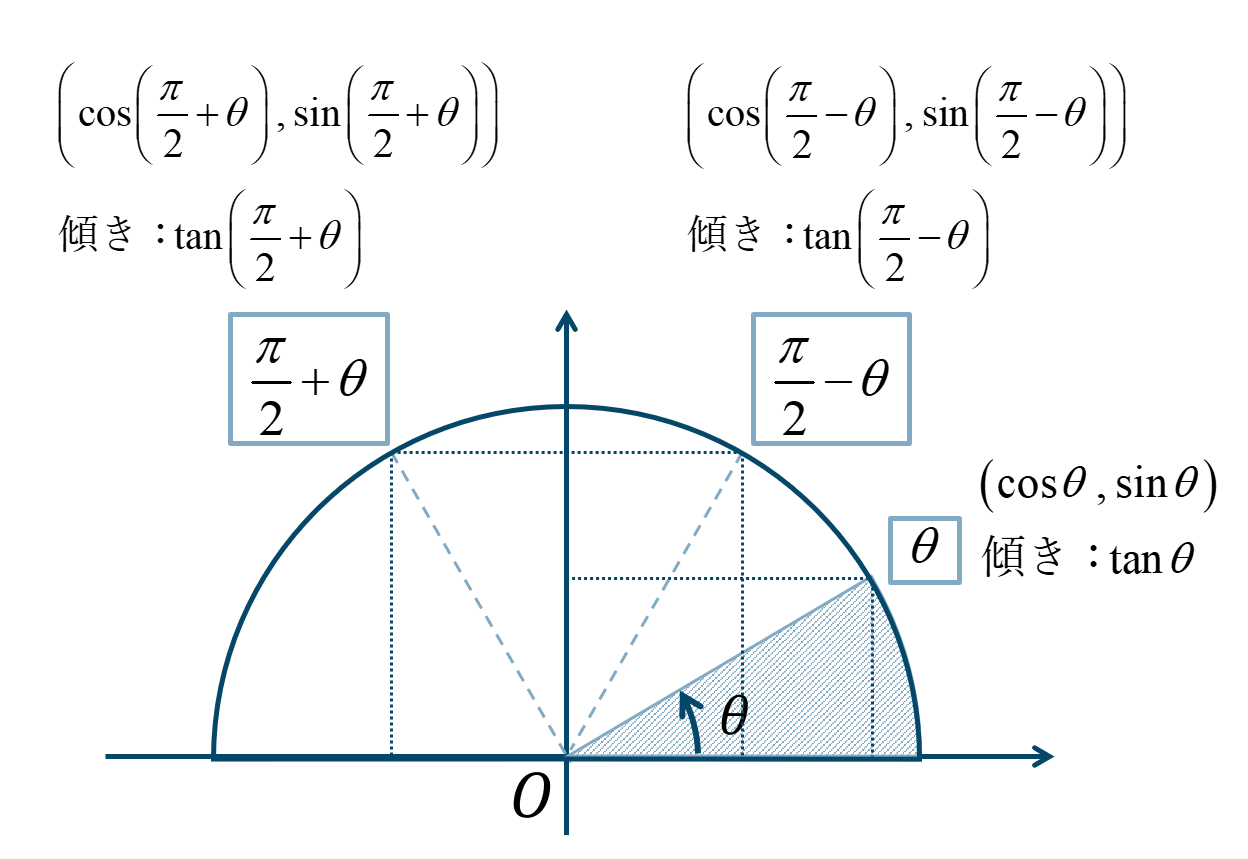



数学 P 2 8 P 2 8の三角関数の求め方とコツ ページ 2 教科書より詳しい高校数学




Y Cos 8 P 2 のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア



三角関数では Cos8 Sin P 2 8 と書くことが出来て Tan8 Sin8 Cos8 Sin8 Sin P 2 8 として表すことが出来るのに なぜcos8 Tan8が必要でしょうか Quora



Q Tbn And9gcsxouhhiiri3r15ey3vur3hb 7bpfdfqjxdwpekftj7smeakvkx Usqp Cau




三角関数の知識 やさしい電気回路




1 の解説の8 3分のp 2分のp はどこから出てきたのですか Clear




置換積分はなぜ置換するのか コツは2つのタイプを区別すること ラディカル高校数学
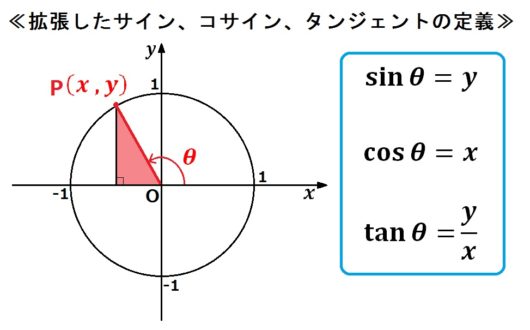



ド文系が 三角比の拡張 と ラジアン をわかりやすく解説する
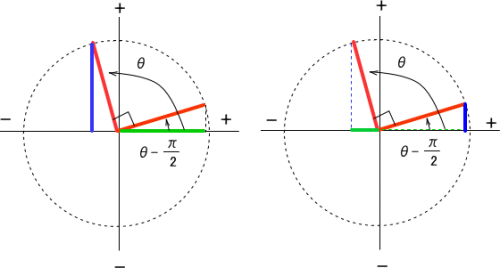



Cos 8 P 2 Sin8 Sin 8 P 2 Cos8 になるんですか Cos 8 P 2 Sin8 数学 教えて Goo




三角関数の性質 8 P 2の角の公式の証明 数学ii By ふぇるまー マナペディア
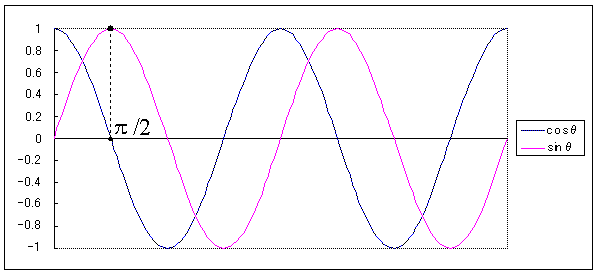



三角関数



逆三角関数をなぜ学ぶか その微分と積分計算への応用 趣味の大学数学




高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット
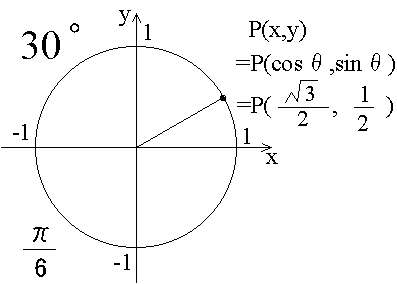



三角関数



数2 三角関数 性質
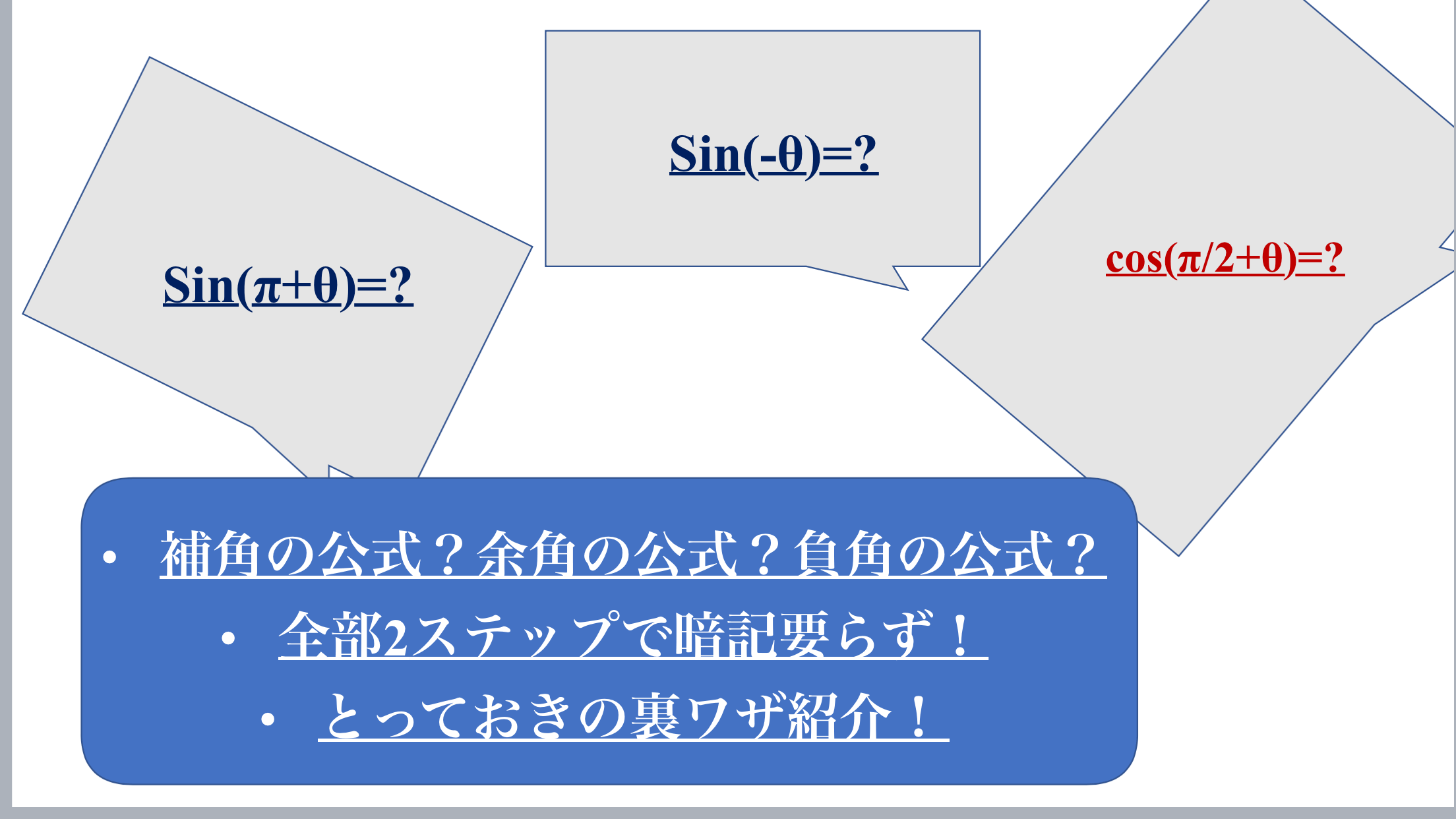



Sin 8 P 2 や90 8など還元公式の覚え方の解説 余角 補角の攻略
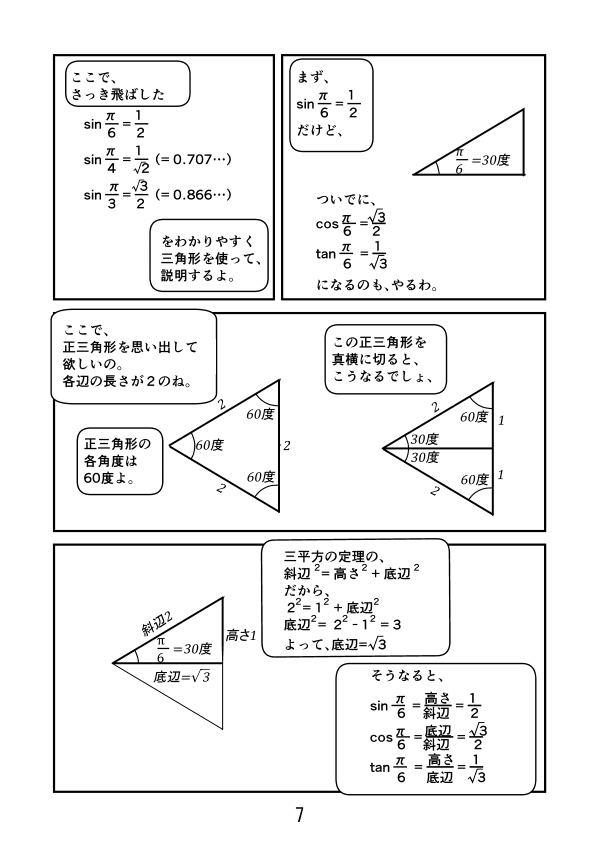



漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100
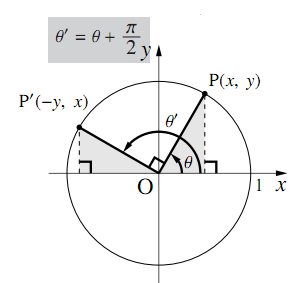



8 P 2の三角関数 数学ii フリー教材開発コミュニティ Ftext
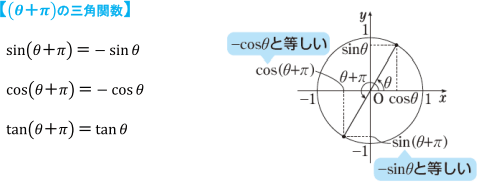



複素数平面 複素数の極形式 数学 定期テスト対策サイト




8 2np 8 8 P 8 P 2 P 8 P 2 8の三角関数 数学ii 三角関数 7 Youtube




高校数学 8 と 8 P 8 Pの関係 映像授業のtry It トライイット
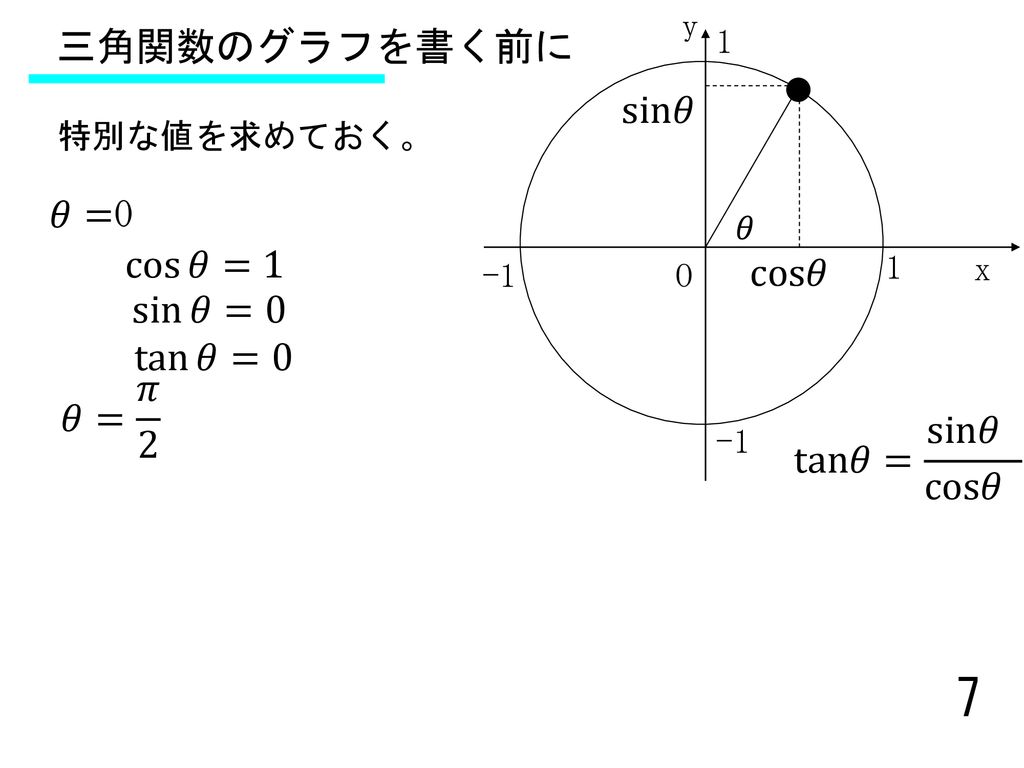



振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download




Y Sin 8 P 2 のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア



三角形の辺の比による三角関数の定義



48s96ub7b0z5f Net Sankakukansuu Seishitsu




標準 三角関数のグラフ なかけんの数学ノート
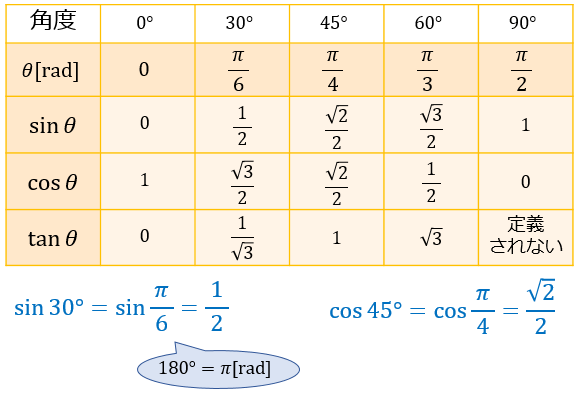



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
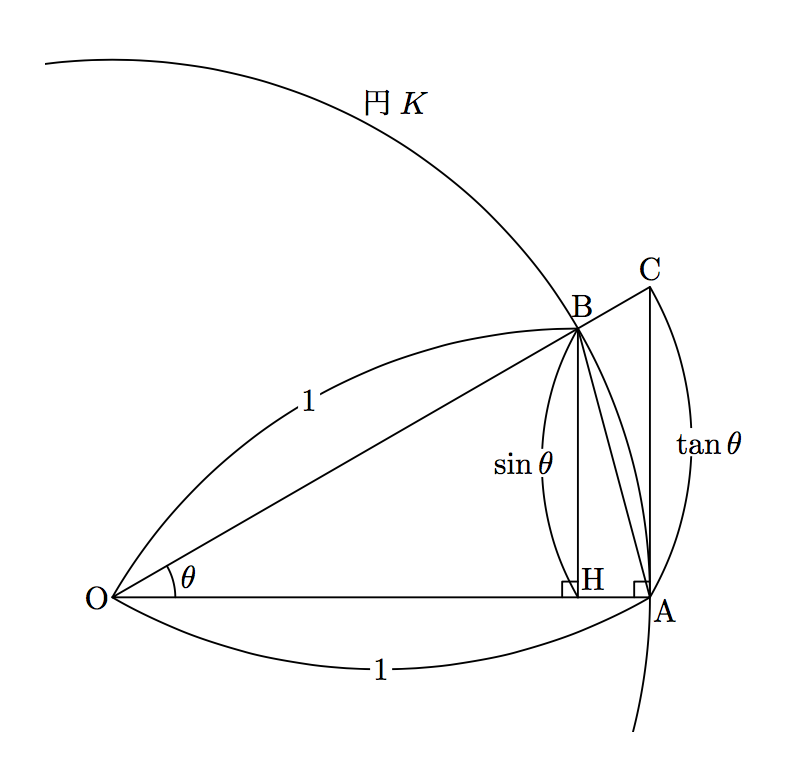



Sin8 8 1 の高校での証明は循環論法ではない Saitei Net




Cos 8 P 2 Sin8 Sin 8 P 2 Cos8 Cos 8 P 2 Sin8 S Cos 8 P 2 S 数学 教えて Goo



0 件のコメント:
コメントを投稿